코딩 인터뷰 완전 분석
자료 구조
해시테이블

- 해시테이블은 효율적인 탐색을 위해 Key를 Value에 대응시킴
해시테이블 구현 방법
1. 키와 해시 코드 계산
> 키의 개수: 무한대, 해시 코드: int, long
> 서로 다른 키가 같은 해시 코드를 가리킬 수 있음
2. hash(key) % array_length 방식을 이용해 배열의 인덱스를 구함
3. 각 배열의 인덱스는 키와 값으로 이루어진 연결리스트 존재
해당 방법 사용 시, 주어진 키로 해시 코드를 계산하여 인덱스 계산
> 충돌이 자주 발생할 경우, 최악의 수행 시간은 O(N)이 됨
> 일반적으로는 O(1)
> 이진 트리로 구현 시, 탐색 시간: O(logN)
ArrayList
- 특정 언어에서는 크기를 자동으로 조절 가능 (동적)
- O(1)의 접근시간
- 배열이 가득 차는 순간 배열의 크기를 두 배로 늘림
> 늘릴 때, O(n)의 시간 발생
> 상환 입력 시간 시 O(1)
상황 입력 시간
- 배열의 크기를 K로 늘리면 그 전 배열의 크기는 K의 절반이므로 K/2만큼의 원소 복사
- N개의 원소를 삽입하기 위해 복사해야하는 총 원소의 개수: N/2 + N/4 + N/8 + ... + 2 + 1 = N 보다 작음
> N개의 원소를 삽입할 때 소요되는 작업 = O(N)
> 평균적인 삽입: O(1)
StringBuilder
문자열을 이어붙일 때마다 두 개의 문자열을 읽은 후, 문자를 새로운 문자열에 복사해야 함
> 총 수행 시간 O(xn^2): 1 + 2 + ... + n = n(n+1)/2 또는 O(n^2)
- StringBuilder: 가변 크기 배열을 이용해 필요한 경우에만 문자열 복사
연결리스트

- 배열과는 달리 연결리스트에서 특정 인덱스를 상수 시간에 접근할 수 없음
- 재귀 호출에 의존
> O(n)의 공간 활용
Runner 기법
Runner: 부가 포인터
> 연결리스트 순회할 때 두 개의 포인터 동시에 사용
> 한 포인터가 다른 포인터보다 앞서거나 따라오는 포인터를 여러 노드를 한 번에 뛰어넘도록 설정할 수 있음
스택과 큐
스택(stack)
- LIFO, 가장 최근에 추가한 항목이 가장 먼저 제거
스택 연산
- pop(): 스택에서 가장 위에 있는 항목 제거
- push(item): item을 가장 윗 부분에 추가
- peek(): 스택의 가장 위에 있는 항목 반환
- isEmtpy(): 스택이 비어 있을 때 true 반환
특징
- 상수 시간에 i번째 항목에 접근 할 수 없음
- 데이터를 추가하거나 삭제하는 연산은 상수 시간에 가능
- 재귀 알고리즘 사용 시 유용
큐(queue)
- FIFO, 큐에 추가된 순서대로 제거
큐 연산
- add(item): item을 리스트 끝부분에 추가
- remove(): 리스트의 첫 번째 항목 제거
- peek(): 큐에서 가장 위에 있는 항목 반환
- isEmpty(): 큐가 비어 있을 때 true 반환
특징
- 너비 우선 탐색 또는 캐시 구현 시 사용
트리와 그래프
트리
- 노드로 이루어진 자료구조
class Tree{
public Node root;
}
특징
1. 하나의 루트 노드를 가짐
- 루트 노드는 0개 이상의 자식 노드를 가짐
- 자식 노드는 0개 이상의 자식 노드를 가짐 (반복적으로 정의)
2. 사이클(cycle)이 존재할 수 없음
- 특정 순서로 나열될 수 없음
이진 트리
각 노드가 최대 두 개의 자식을 갖는 트리
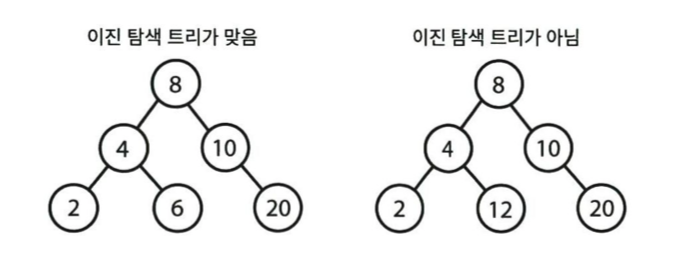
이진 탐색 트리
모든 왼쪽 자식들 <= n < 모든 오른쪽 자식들
균형 트리
- O(logN) 시간에 insert와 find를 할 수 있는 트리
ex) 레드블랙트리, AVL트리
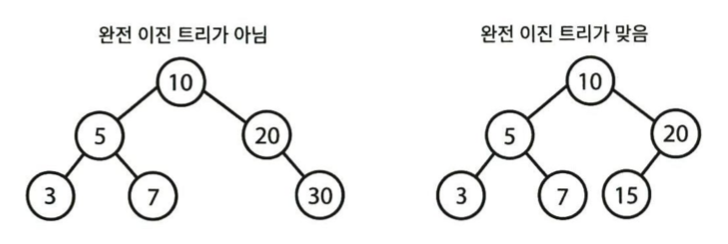
완전 이진 트리
모든 높이에서 노드가 꽉 차있는 이진 트리
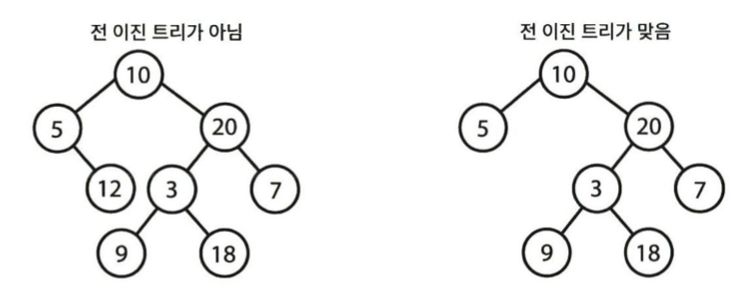
전 이진 트리
모든 노드의 자식이 없거나 정확히 두 개 있는 경우, 자식이 하나만 있는 노드가 존재하지 않음
포화 이진 트리
전 이진 트리 이면서 완전 이진 트리인 경우
- 노드의 개수: 2^(k-1), k는 트리의 높이
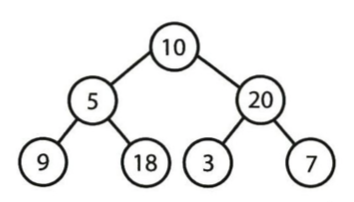
이진 트리 순회
- 중위 순회: 왼쪽 - 현재 노드 - 오른쪽을 방문 후 출력
- 전위 순회: 자식 노드보다 현재 노드를 먼저 방문
- 후위 순회: 모든 자식 노드를 먼저 방문한 뒤 마지막 현재 노드 방문
이진 힙
최소힙: 오른쪽 부분을 뺀 나머지 부분이 가득 채워져 있는 완전 이진 트리, 각 노드의 원소가 자식 원소보다 작음
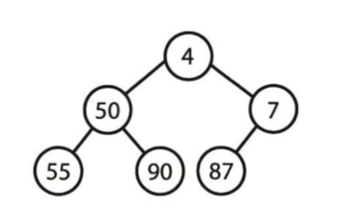
삽입 연산
- O(log n)
1. 트리의 밑바닥 가장 오른쪽 위치에서 부터 삽입
2. 삽입된 원소가 제대로 된 자리를 찾을 때까지 부모 노드와 교환
3. 최소 원소를 위쪽으로 올림
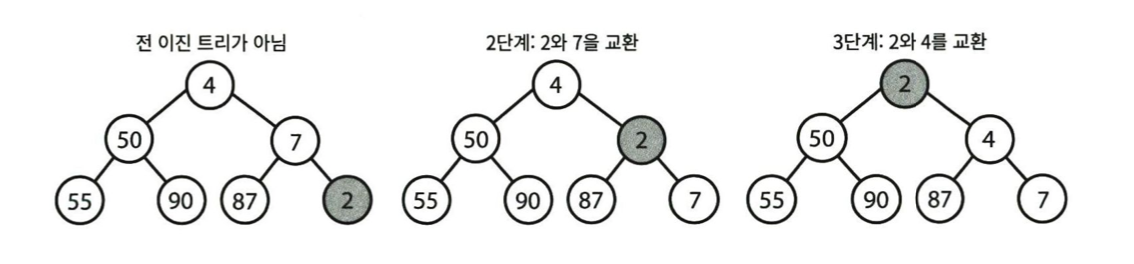
최소 원소 뽑아내기
- O(log n)
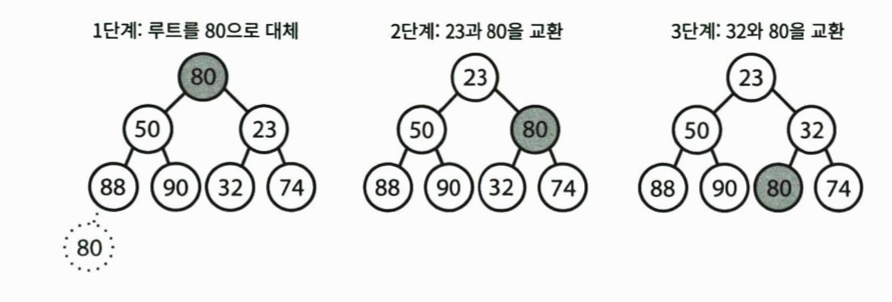
1. 루트 노드를 제거(루트 = 최소 원소)
2. 최소 원소를 제거한 후, 가장 마지막 왼쪽 원소와 교환
3. 최소 힙에 만족하도록 해당 노드를 자식 노드와 교환하여 밑으로 보냄
- 왼쪽과 오른쪽 중 더 작은 원소와 교환
접투사 트리(트라이, trie)
각 노드에 문자를 저장하는 자료 구조, n-차 트리의 변형
접두사를 빠르게 찾아보기 위해 사용
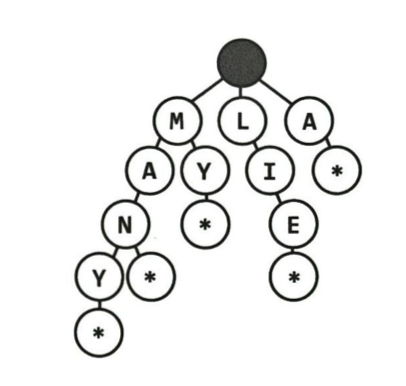
특징
- null node(* 노드): 단어의 끝을 나타냄
ex) MANY*: MANY단어의 완성
- 각 노드는 1개에서 Alphabet_size + 1개까지의 자식을 가짐(*노드)
- 길이가 K인 문자열을 O(K)의 시간에 접두사를 확인할 수 있음
> 해시테이블을 사용하는 것과 같은 수행 시간
그래프
노드와 노드를 연결하는 간선을 하나로 모아 놓은 것
트리, 단방향 그래프, 양방향 그래프, 연결 그래프(모든 정점 간에 경로가 존재), 비순환 그래프 등
그래프 표현
1. 인접 리스트
- 모든 정점을 인접 리스트에 저장
- 인접한 간선을 저장
2. 인접 행렬
- N*N 행렬을 matrix[i][j]가 true일 때 i에서 j로 간선이 존재
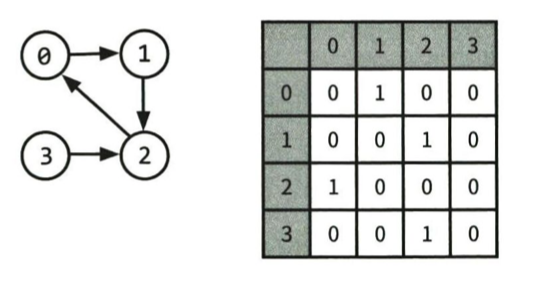
- 너비 우선 탐색 시, 인접 행렬에서는 효율성이 떨어짐
그래프 탐색
1. 깊이 우선 탐색(DFS)
루트 노드에서 시작해서 다음 분기로 넘어가기 전 해당 분기를 완벽하게 탐색하는 방법
- 모든 노드 방문 시 사용
2. 너비 우선 탐색(BFS)
루트 노드에서 시작한 인접 노드를 먼저 탐색하는 방법
- 임의의 경로 시 사용
3. 양방향 탐색
출발지와 도착지 사이 최단 경로를 찾을 때 사용
- 출발지와 도착지에서 동시에 너비 우선 탐색 실행 후, 두 탐색 지점이 충돌할 때 경로를 찾음
- 두 탐색 알고리즘이 대략 d/2단계(출발지와 도착지의 중간 지점)에서 탐색 후 충돌 -> 방문하게 되는 전체 노드는 약 2*k^d/2, O(k^d/2)개
'IT > 책' 카테고리의 다른 글
| [데이터설계] 2장, 데이터 모델과 질의 언어 (0) | 2022.08.13 |
|---|---|
| [코딩인터뷰] 자료구조 - 배열과 문자열 해법 (0) | 2022.01.30 |
| [Clean Architecture] 1달1권, 두번째 책 후기 (0) | 2022.01.07 |
| [Clean Architecture] 6부, 세부사항 (0) | 2021.12.26 |
| [Clean Architecture] 5부, 아키텍처 (2) (0) | 2021.12.19 |
