문제
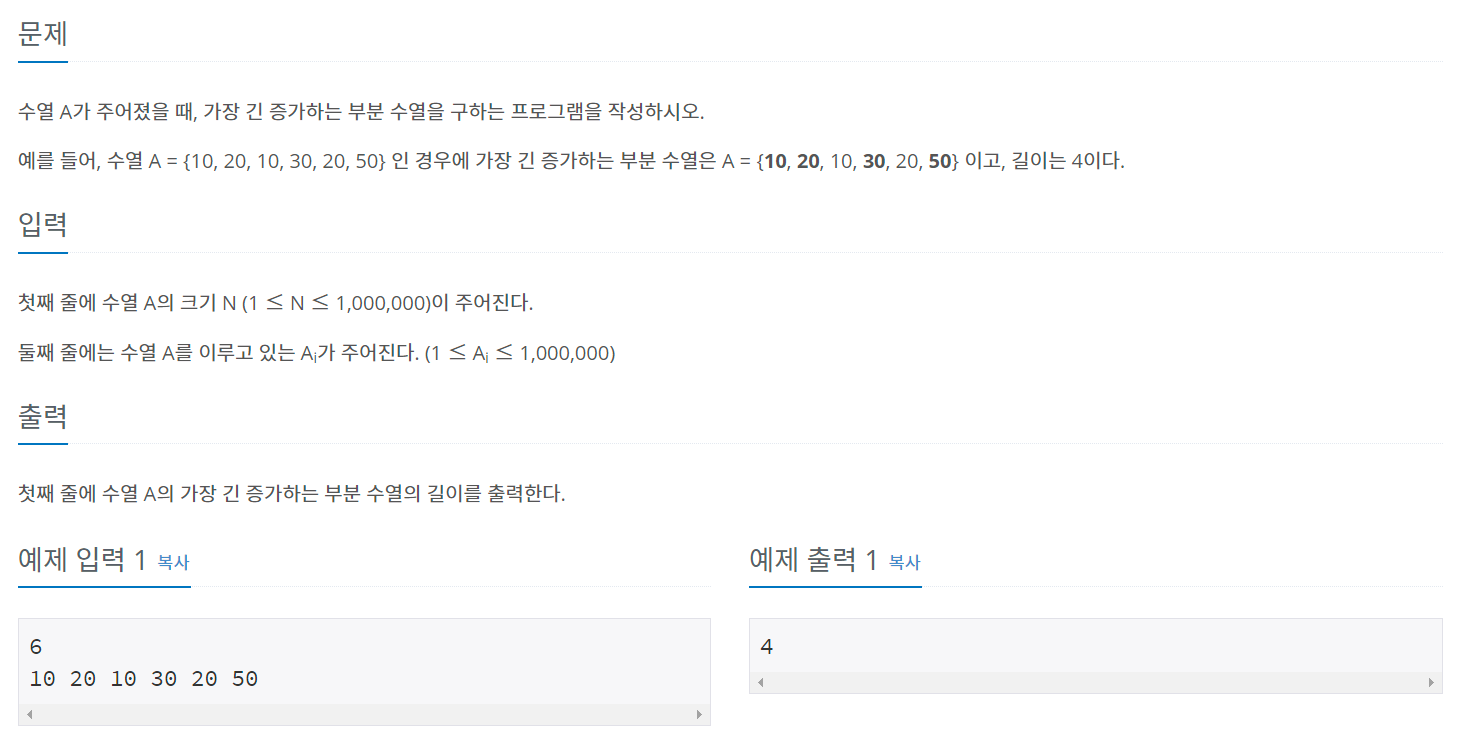
LIS라는 대표적인 알고리즘 문제 중 하나이다. 가장 긴 증가하는 부분 수열의 길이를 리턴한다.
가장 긴 증가하는 부분수열 11053 문제는 O(n^2)으로 문제를 풀 수 있지만, 해당 문제는 O(nlogn)의 시간으로 코드를 짜야한다.
https://jason9319.tistory.com/113 이 블로그에 설명이 잘 나와있지만, 공부하는 마음으로 작성한다.
해설 및 코드
- Lower Bound는 O(logn)의 시간을 소모한다. 이러한 이분탐색의 일종인 Lower Bound를 이용하여 O(nlogn)의 시간으로 해결한다.
package BAEKJOON;
import java.util.ArrayList;
import java.util.Scanner;
public class 가장긴증가하는부분수열2_12015 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int[] arr = new int[N];
for (int i = 0; i < arr.length; i++) {
arr[i] = sc.nextInt();
}
ArrayList<Integer> rs = new ArrayList<>();
rs.add(arr[0]); //ArrayList를 empty로 만들지 않는다.
//O(n) * O(logn) = O(nlogn)
for (int i =1 ; i < arr.length; i++) {
int lower = lowerBound(rs, 0, rs.size(), arr[i]);
//삽입할 위치가 맨 뒤일 때
if(rs.size() <= lower) rs.add(arr[i]);
//삽입할 위치에 이미 숫자가 존재하면 바꾼다.
else rs.set(lower, arr[i]);
}
System.out.println(rs.size());
}
// Basic한 Lower Bound 코드
public static int lowerBound(ArrayList<Integer> arr, int left, int right, int key) {
int mid = 0;
while (left < right) {
mid = (left + right) / 2;
if (arr.get(mid) < key)
left = mid + 1;
else
right = mid;
}
return right;
}
}
배열을 탐색하면서 만들 수 있는 가장 긴 수열을 만들면서 진행한다.
arr 배열이 [10, 20, 10, 30, 20, 50]이 존재한다고 할 때,
rs는
10 [10] ➡ 20 [10, 20] ➡ 10 [10, 20] ➡ 30 [10, 20, 30] ➡ 20 [10, 20, 30] ➡ 50 [10, 20, 30, 50]
와 같이 배열이 변한다.
lower bound의 성질에 의해 내 현재 Key(arr[i]번째 수)보다 작은 위치를 return 한다.
위와 같이 배열을 만들면서 갈 수가 있는 것은, 배열을 진행하면서 만들 수 있는 가장 긴 증가하는 부분수열을 만들기 때문이다.
arr[i]의 숫자보다 작아야하니까, arr[i]보다 큰 숫자의 위치를 arr[i]가 빼았는다.
📍 그러나 rs가 올바른 LIS 배열을 가지지는 않는다.
[10, 20, 25, 18, 50]인 배열일 때,
rs는
10 [10] ➡ 20 [10, 20] ➡ 25 [10, 20, 25] ➡ 18 [10, 18, 25] ➡ 50 [10, 18, 25, 50]
와 같이 배열이 변한다.
밑줄 친 배열의 부분은 18보다 25가 더 먼저 나타나있으므로, 올바른 증가하는 부분 수열이라고 할 수 없다.
그러나 개수만 보기 때문에 상관 없다. 20의 역할을 18이 잠시 맡고 있는 것이다.
이후에 18과 25 사이의 숫자가 나타나더라도, 25보다 작은 숫자가 제일 마지막을 차지하면 되고, 18은 자연스럽게 증가하는 부분 수열을 이루는 원소로 작용할 수 있다.
Java 문법 정리
public static int lowerBound(int[] arr, int left, int right, int key){
int mid = 0;
while(left<right){
mid = (left+right)/2;
if(arr[mid]< key) left = mid+1;
else right = mid;
}
return right;
}public static int upperBound(int[] arr, int left, int right, int key){
int mid = 0;
while(left<right){
mid = (left+right)/2;
if(arr[mid]<=key) left=mid+1;
else right=mid;
}
return right;
}
TreeSet을 이용한 Lower Bound와 Upper Bound
TreeSet<Integer> ts = new TreeSet<>();
Integer lower = ts.lower(Key);
Integer upper = ts.higher(Key);
'IT > 알고리즘' 카테고리의 다른 글
| [프로그래머스] 종이접기 - Cos Pro 1급 (0) | 2022.04.20 |
|---|---|
| [BOJ] 순회강연 2109.java (0) | 2021.06.21 |
| [BOJ] 합이0 3151.java (0) | 2021.06.01 |
| [BOJ] 시리얼번호 1431.java (0) | 2021.05.18 |
| [BOJ] 배열돌리기1_16926.java (0) | 2021.04.09 |



